Droplet breakup in junctions | Yves-Marie Ducimetière

In Microfluidics, the breakup of a droplet into comparatively smaller ones is often the first step to achieving more versatile functionalities. In this project, we considered unconventional T-junctions whose outlet channels have a smaller dimension than the inlet channel (see Fig. 1a).

Figure 1. (a) Geometry of the T-junctions used throughout our study: Both aspect ratio \(h/w_o\) and width ratio \(w_i/w_o\) are larger than unity. (b) Time sequence of a lateral breakup process for an initially short (blue) and a long (red) droplet. The inset shows the interface at the moment of the breakup (indicated by the red arrow).

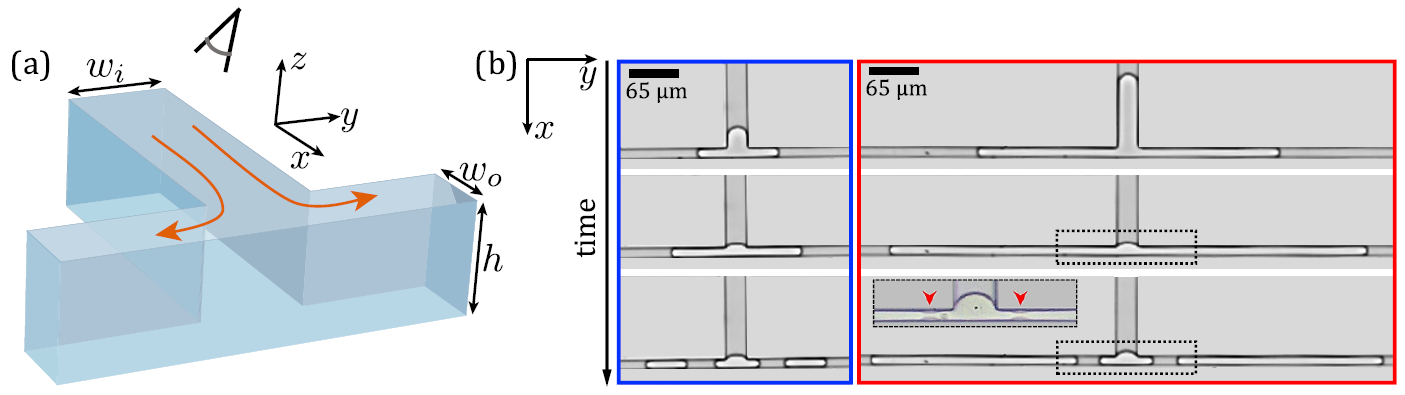
In a region of the parameter space, we reported in (Zhou et al., 2023) a novel droplet breakup regime in which the droplet interface breaks symmetrically in the two outlet channels and far from the junction (see Fig. 1b), rather than at its center, as would occur for a conventional T-junction (where the outlet and inlet channels have the same dimension). This leads to the formation of three daughter droplets instead of two. This new breakup phenomenon, which we called a “ lateral breakup ”, is driven by an unbalanced capillary pressure at the droplet interface, induced by the strong gradient of confinement across the junction (provided \(h>w_i>w_o\) in Fig.1a). In other terms, this breakup phenomenon is driven by surface tension!

By increasing the capillary number \(Ca\), hydrodynamic-stress-driven mechanisms become dominant over the surface-tension-driven ones mentionned above. Therefore, above a certain threshold value \(Ca^*\), the lateral breakup regime is not observed anymore, but one in which the droplet breaks in the center (“ central breakup ”) is found instead (see Fig. 2). The latter regime is commonly observed in T-junctions without gradient of confinement.

Figure 2. Time sequences of example breakup events for the same droplet length under three flow conditions. The breakup regime shifts from lateral to central breakup from low to high \(Ca\). The scale bar represents 30 \(\mu m\).

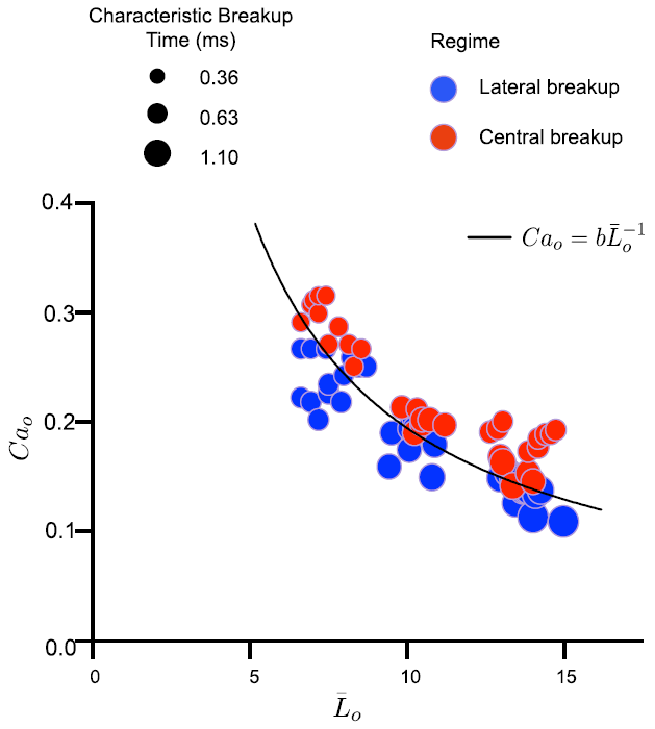
Crucially, the critical capillary number \(Ca^*\), above which the central breakup is observed, was found to depend on the (mother) droplet length according to a \(-1\) power law (see Fig. 3).

Figure 3. The breakup transition regime map of \(C_{a_o}=C_a(w_i/w_o)/2\) versus \(\overline{L}_o\), the nondimensional initial length of the droplet. Blue and red circles represent lateral and central breakups, respectively. The black curve represents the function \(C_{a_o} \propto \overline{L}^{-1}_o\).

To capture these two (lateral and central) breakup phenomena, François Gallaire, Ludovic Keiser , and I have developed and presented in (Zhou et al., 2023) a theoretical model. As the droplet advances inside the channel, our model can qualitatively predict the formation and inflation of lateral pockets, where the continuous phase accumulates in volume much larger than that in the gutters. This indeed culminates in a lateral breakup of the droplet. Unfortunately, the validity of the model was found to be restricted to low \(Ca\) values, and it could not capture the transition to a central breakup regime for larger \(Ca\).

At large \(Ca\), elements which we did not account for in (Zhou et al., 2023) must be incorporated into the model (e.g., viscous dissipation, and a better description of the cross-section occupancy of both liquids). Numerical simulations, for instance, can help identify which ones! My former colleague at EPFL, Tomas Fullana is currently working on that! For my part, even though I am no longer actively working on this project, the complexity of this flow continues to fascinate me, and I intend to delve into it again in the future.

References

2023